Runge-Kutta Method
Runge-Kutta 방법은 초기값initial value 조건을 가지는 상미분 방정식ordinary differential equations을 푸는 데 사용되는 대표적인 방법 중 하나입니다.
초기값 문제는 일반적으로 초기 조건이 주어질 때, 미분 방정식을 통해 나중의 값을 찾는 문제입니다.
예를 들어 초기 위치와 속도가 주어지고 가속도 $a$가 시간 $t$, 위치 $x$, 속도 $v$에 대한 함수임이 알려져 있다고 합시다.
이때 가속도를 다음과 같이 쓸 수 있습니다:
$$
\frac{d^2x}{dt^2} = a(t, x, v).
$$
단순한 등가속도 운동의 경우 $a$는 항상 일정한 값을 가질 것입니다.
용수철에 연결된 물체의 운동의 경우 $a$는 $x$에 대한 함수일 것입니다.
그밖에 저항을 고려하거나 시간에 따른 힘이 주어질 때 $a$는 $t$, $v$에 대한 식을 포함할 수 있을 것입니다.
위의 이차 미분 방정식은 속도 $v$를 이용하여 두 개의 일차 미분 방정식으로 바꿀 수 있습니다:
$$
\frac{dv}{dt} = a(t, x, v), \quad \frac{dx}{dt} = v.
$$
위의 방정식에서 우리는 두 개의 변수 $x$, $v$를 시간에 따라 적분해야 합니다.
이를 묶어서 행렬 형태로 나타내는 것이 편합니다. 예를 들어 임의의 시간 $t_n = n\Delta t$에서의 값을 다음과 같이 쓰고,
$$
\bold{y}_n = \begin{pmatrix}
x_n \\
v_n
\end{pmatrix},
$$
미분 방정식은 다음과 같이 씁니다:
$$
\frac{d}{dt}\bold{y}_n = \begin{pmatrix}
v_n \\
a_n
\end{pmatrix}.
$$
이제 주어진 초기 위치와 속도를 하나의 변수 $\bold{y}$로 보고 위의 방정식을 이용하여 시간에 따라 새로운 값으로 갱신할 수 있습니다.
Euler Method
Euler 방법은 미분 방정식을 해결하는 아주 기본적이고 직관적인 방법입니다.
이 방법은 다음 식과 같이 $\bold{y}$를 갱신합니다:
$$
\bold{y}_{n+1} = \bold{y}_n + \Delta t \left(\frac{d}{dt}\bold{y}_n\right) + \mathcal{O}((\Delta t)^2).
$$
위의 식은 $\bold{y}$를 $t_n$에서 테일러 전개하여 얻을 수 있으며 $(\Delta t)^2$ 이후의 항을 무시하므로 $1$차 정확도를 가집니다.
이를 파이썬 코드로 나타내면 다음과 같습니다. 여기서 가속도는 질량과 용수철 상수가 모두 $1$인 단순 조화 진동자simple harmonic oscillator가 되도록 하였습니다.
따라서 주기는 $2\pi \approx 6.28$, 진폭은 $1$이 되어야 합니다.
# Set time step interval, initial t, y = [x, v]
dt = 0.1
t = 0
y = [0, 1]
# SHO. x_dot = v, y_dot = -x
def y_dot(t, *y):
return y[1], -y[0]
# To store data
T = [t]
X = [y[0]]
V = [y[1]]
# Iteration using Euler Method
for n in range(200):
x_dot, v_dot = y_dot(t, *y)
t += dt
y[0] += x_dot * dt
y[1] += v_dot * dt
T.append(t)
X.append(y[0])
V.append(y[1])
결과는 다음과 같습니다.
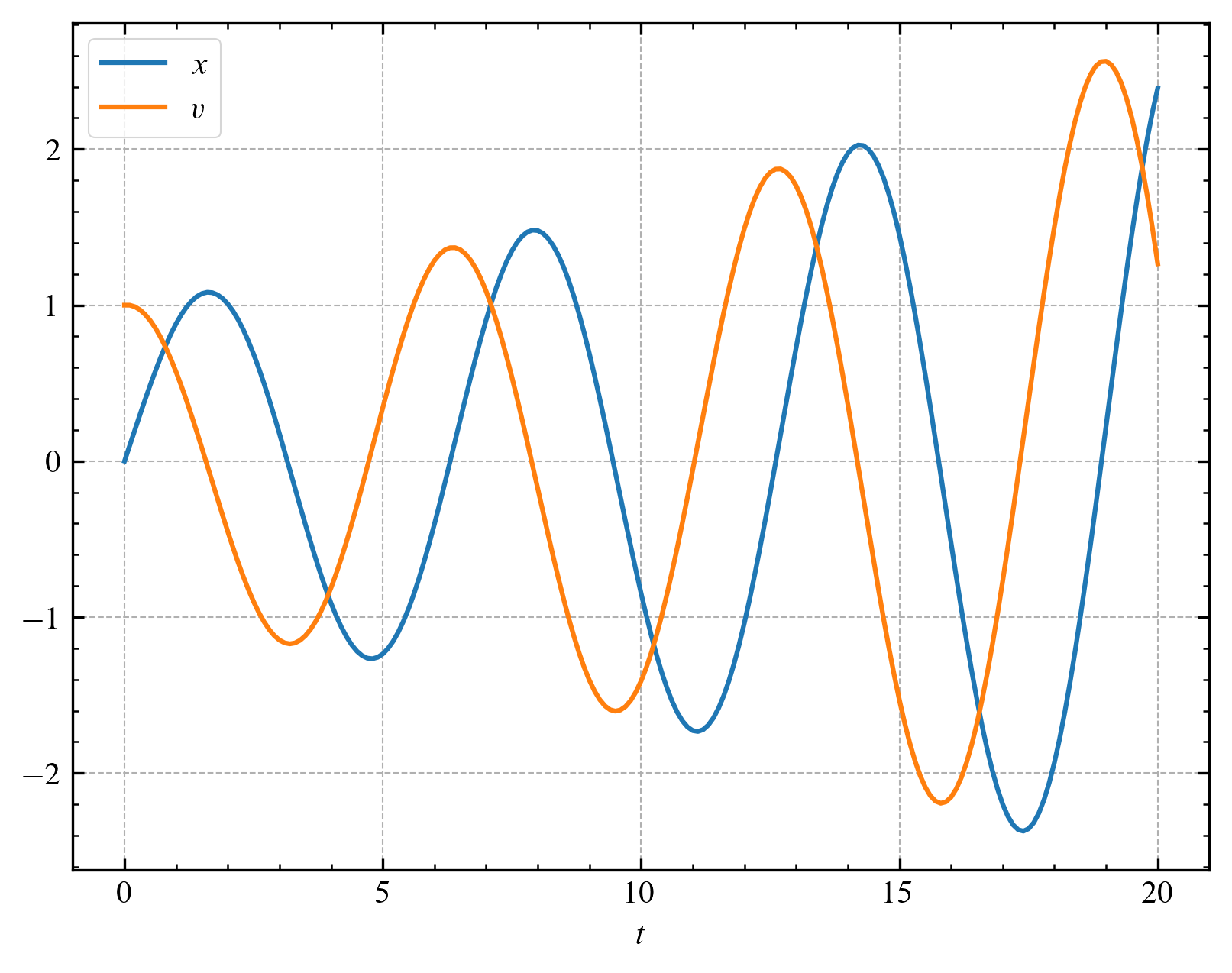 처음에는 진폭이 거의 $1$에 가까운 운동을 보였지만 시간이 지날수록 진폭이 점점 증가하는 모습을 볼 수 있습니다.
시간 간격 $\Delta t$를 줄이면 더 정확한 결과를 얻을 수 있습니다.
다음 그림은 위와 같은 조건에서 $\Delta t$를 $1/10$배로 하고 반복 횟수는 $10$배로 한 모습을 나타낸 것입니다.
처음에는 진폭이 거의 $1$에 가까운 운동을 보였지만 시간이 지날수록 진폭이 점점 증가하는 모습을 볼 수 있습니다.
시간 간격 $\Delta t$를 줄이면 더 정확한 결과를 얻을 수 있습니다.
다음 그림은 위와 같은 조건에서 $\Delta t$를 $1/10$배로 하고 반복 횟수는 $10$배로 한 모습을 나타낸 것입니다.
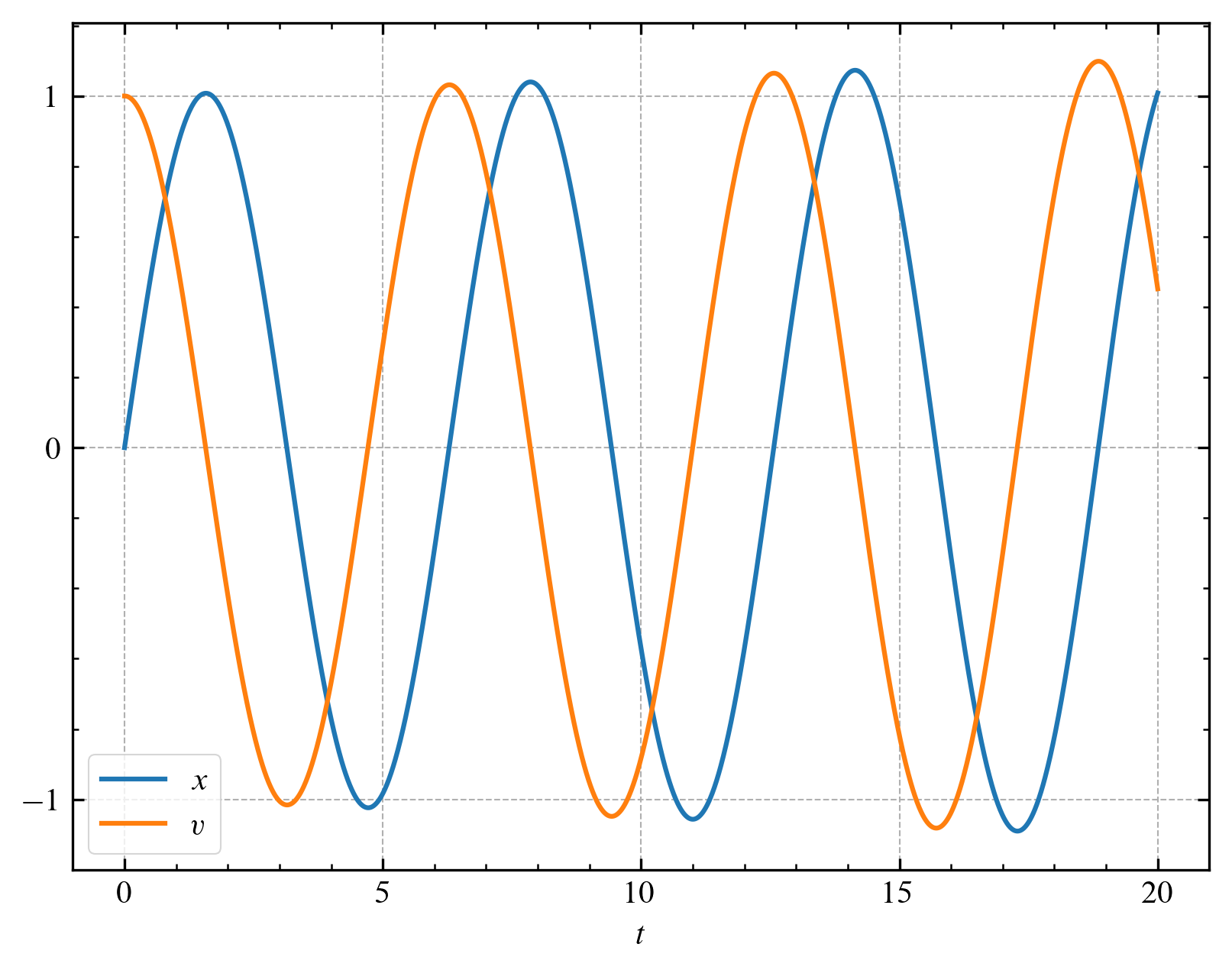 우리는 위 방정식의 해가 $x_\mathrm{ext} = \sin t$, $v_\mathrm{ext} = \cos t$임을 알고 있으므로
상대 오차 $x_\mathrm{err} = |\frac{x - x_\mathrm{ext}}{x_\mathrm{ext}}|$,
$v_\mathrm{err} = |\frac{v - v_\mathrm{ext}}{v_\mathrm{ext}}|$ 또한 나타낼 수 있습니다.
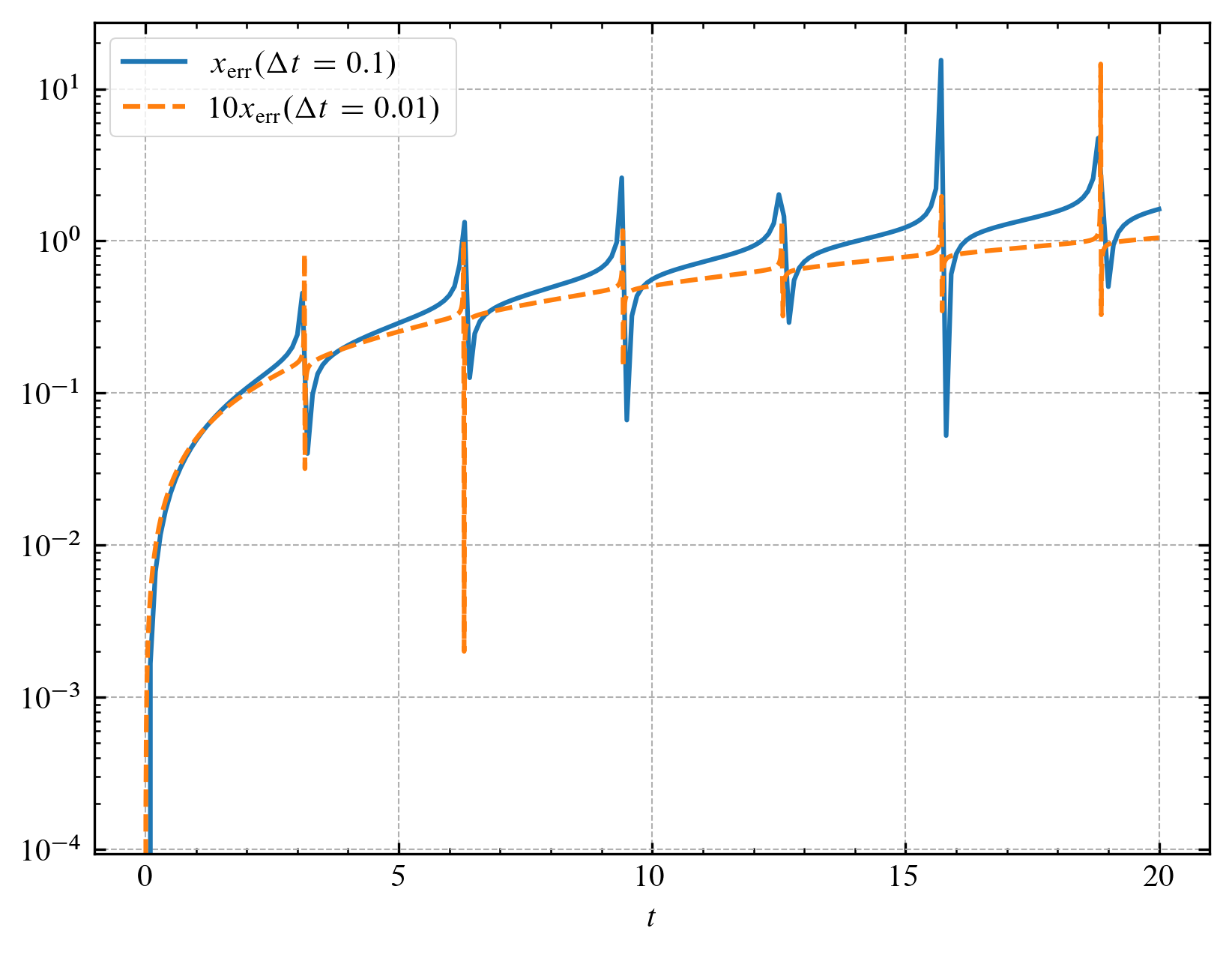
다음 그림은 각각 $\Delta t$가 $0.1$, $0.01$일 때 $x$, $v$의 상대 오차를 나타낸 것입니다.
우리는 위 방정식의 해가 $x_\mathrm{ext} = \sin t$, $v_\mathrm{ext} = \cos t$임을 알고 있으므로
상대 오차 $x_\mathrm{err} = |\frac{x - x_\mathrm{ext}}{x_\mathrm{ext}}|$,
$v_\mathrm{err} = |\frac{v - v_\mathrm{ext}}{v_\mathrm{ext}}|$ 또한 나타낼 수 있습니다.
다음 그림은 각각 $\Delta t$가 $0.1$, $0.01$일 때 $x$, $v$의 상대 오차를 나타낸 것입니다.
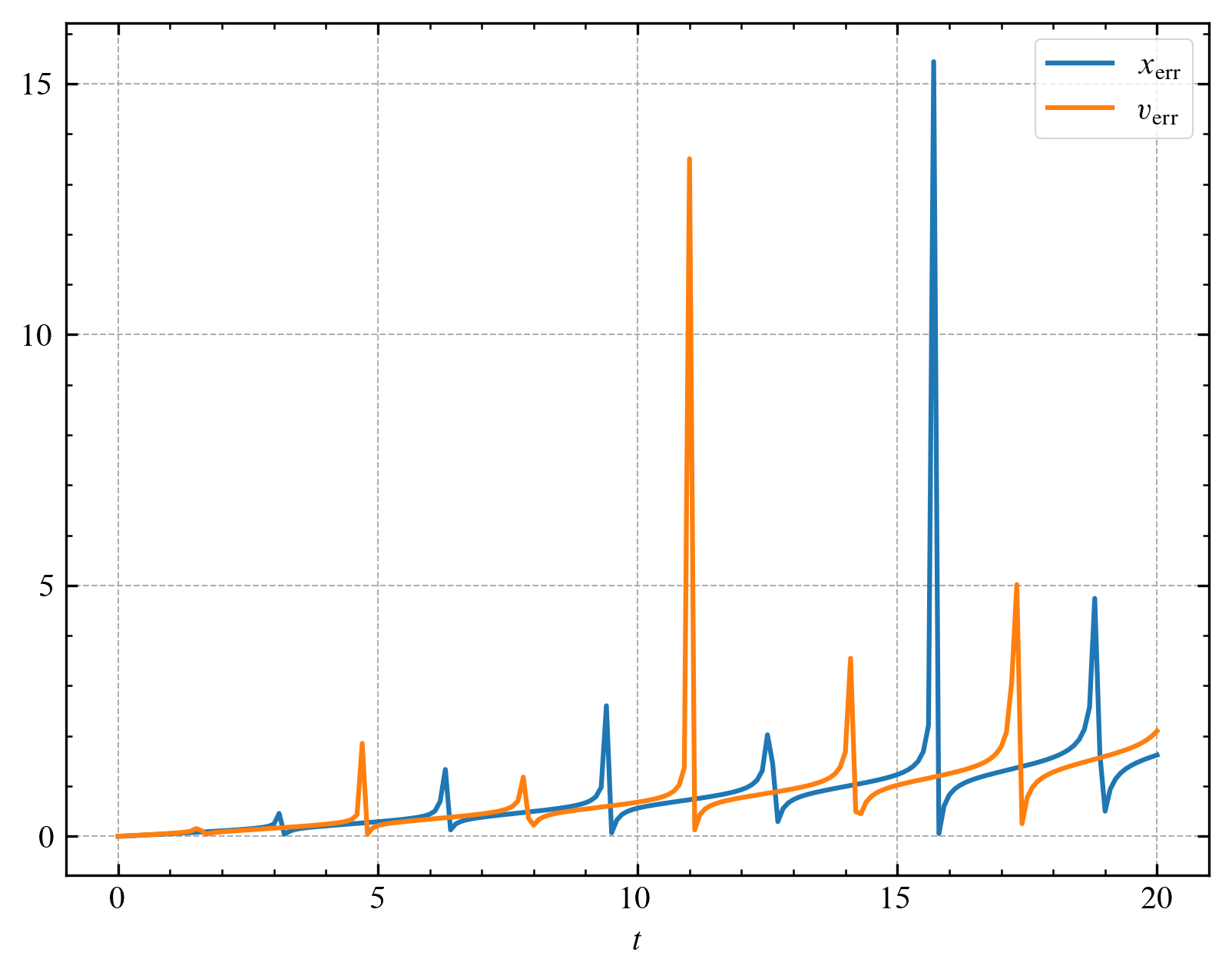
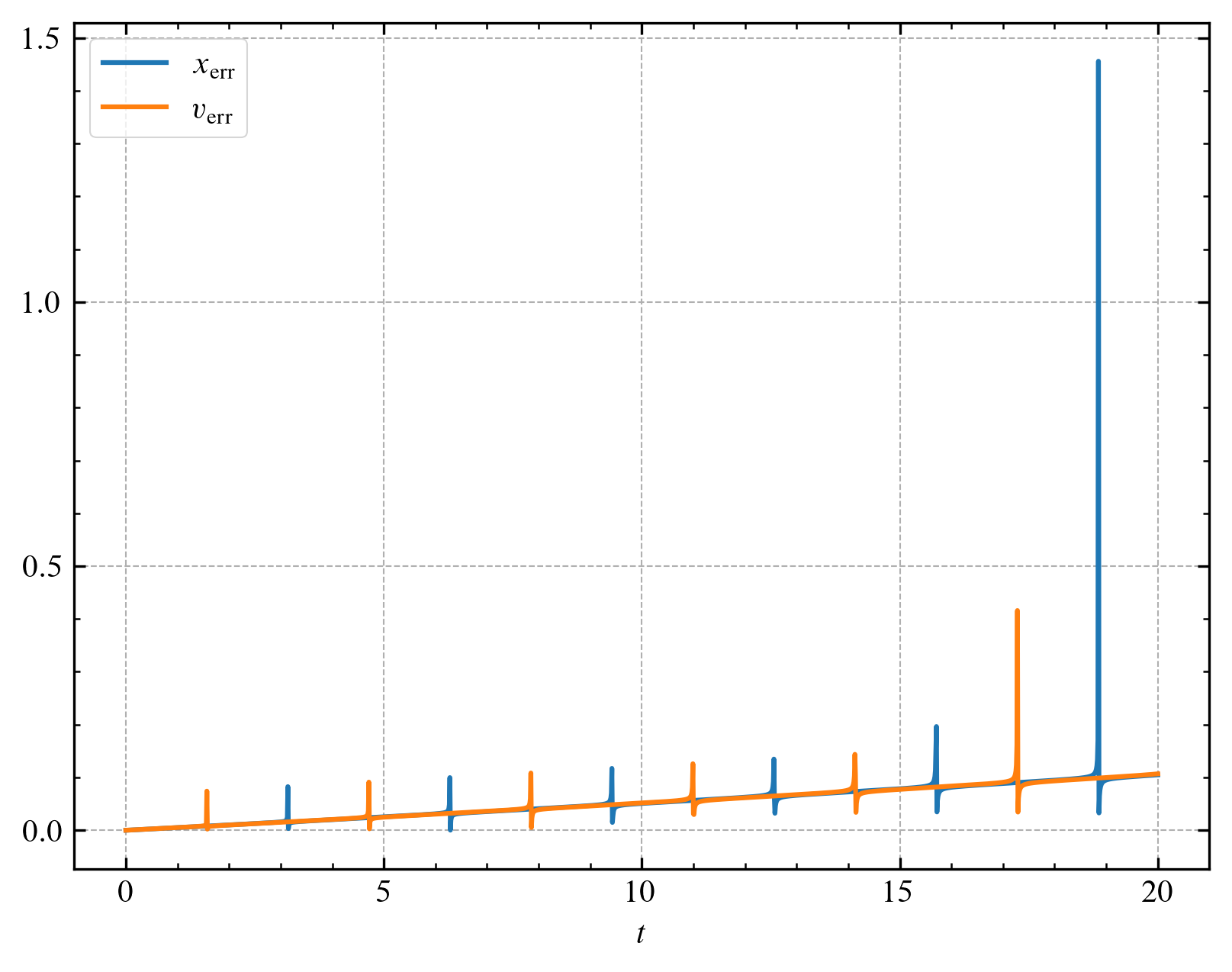 사용한 Euler 방법이 $1$차 정확도를 가지므로 둘의 차이는 대략 $10^{1}$배입니다.
사용한 Euler 방법이 $1$차 정확도를 가지므로 둘의 차이는 대략 $10^{1}$배입니다.
2nd-order Method
$\bold{y}$의 테일러 전개에서 고차항을 사용할수록 더 정확한 결과를 얻을 수 있을 것입니다. 즉 다음 식에서 $\bold{y}_n ''\Delta t^2$을 $\mathcal{O}(\Delta t^3)$의 정확도로 구해내면 됩니다:
$$
\bold{y}_{n+1} = \bold{y}_n + \bold{y}_n'\Delta t + \frac{1}{2}\bold{y}_n''\Delta t^2 + \mathcal{O}(\Delta t ^3).
$$
이를 위해 $t + \Delta t / 2 $에서의 $\bold{y}$를 먼저 구해봅시다.
$$
\bold{y}_{n+1/2} = \bold{y}_n + \frac{1}{2} \bold{y}_n' \Delta t + \mathcal{O}(\Delta t^2).
$$
이로부터 $\bold{y}_{n}'$을 구하는 것과 마찬가지로 $\bold{y}_{n + 1/2}'$를 얻을 수 있습니다.
한편 $\bold{y}_{n+1/2}'$는 다음과 같이 테일러 전개로 나타낼 수 있습니다:
$$
\bold{y}_{n+1/2}' = \bold{y}_n' + \bold{y}_n'' \frac{\Delta t}{2} + \mathcal{O}(\Delta t^2).
$$
이를 $\bold{y}_n''$에 대해 정리하면
$$
\bold{y}_n'' = \frac{2(\bold{y}_{n+1/2}' - \bold{y}_n')}{\Delta t} + \mathcal{O}(\Delta t)
$$
이고 다시 $\bold{y}$에 대한 식에 넣으면
$$
\begin{align*}
\bold{y}_{n+1} &= \bold{y}_n + \bold{y}_n'\Delta t + \frac{1}{2}\bold{y}_n''\Delta t^2 + \mathcal{O}(\Delta t ^3)\\
&= \bold{y}_n + \bold{y}_n'\Delta t + (\bold{y}_{n+1/2}' - \bold{y}_n')\Delta t + \mathcal{O}(\Delta t ^3)\\
&= \bold{y}_n + \bold{y}_{n+1/2}' \Delta t + \mathcal{O}(\Delta t ^3)
\end{align*}
$$
를 얻습니다. 이를 $2$차 Runge-Kutta 방법이라 합니다.
파이썬 코드로 나타내면 다음과 같습니다. 성분 계산의 번거로움을 피하고자 numpy를 사용하였습니다.
import numpy as np
def rk2(dt=0.1, it=200):
t = 0
y = np.array([0.0, 1.0])
# SHO. x_dot = v, y_dot = -x
def y_dot(t, y):
return np.array([y[1], -y[0]])
# To store data
T = [t]
X = [y[0]]
V = [y[1]]
# Iteration using RK2 Method
for n in range(it):
t += dt
k1 = y_dot(t, y)
k2 = y_dot(t + dt / 2, y + k1 / 2 * dt)
y += k2 * dt
T.append(t)
X.append(y[0])
V.append(y[1])
return np.array(T), np.array(X), np.array(V)
결과는 다음과 같습니다. 앞선 $1$차 정확도를 가졌던 Euler 방법과 같은 시간 간격 $0.1$을 사용하여도 육안으로 구별 불가능한 정도의 정확도를 보여줍니다.
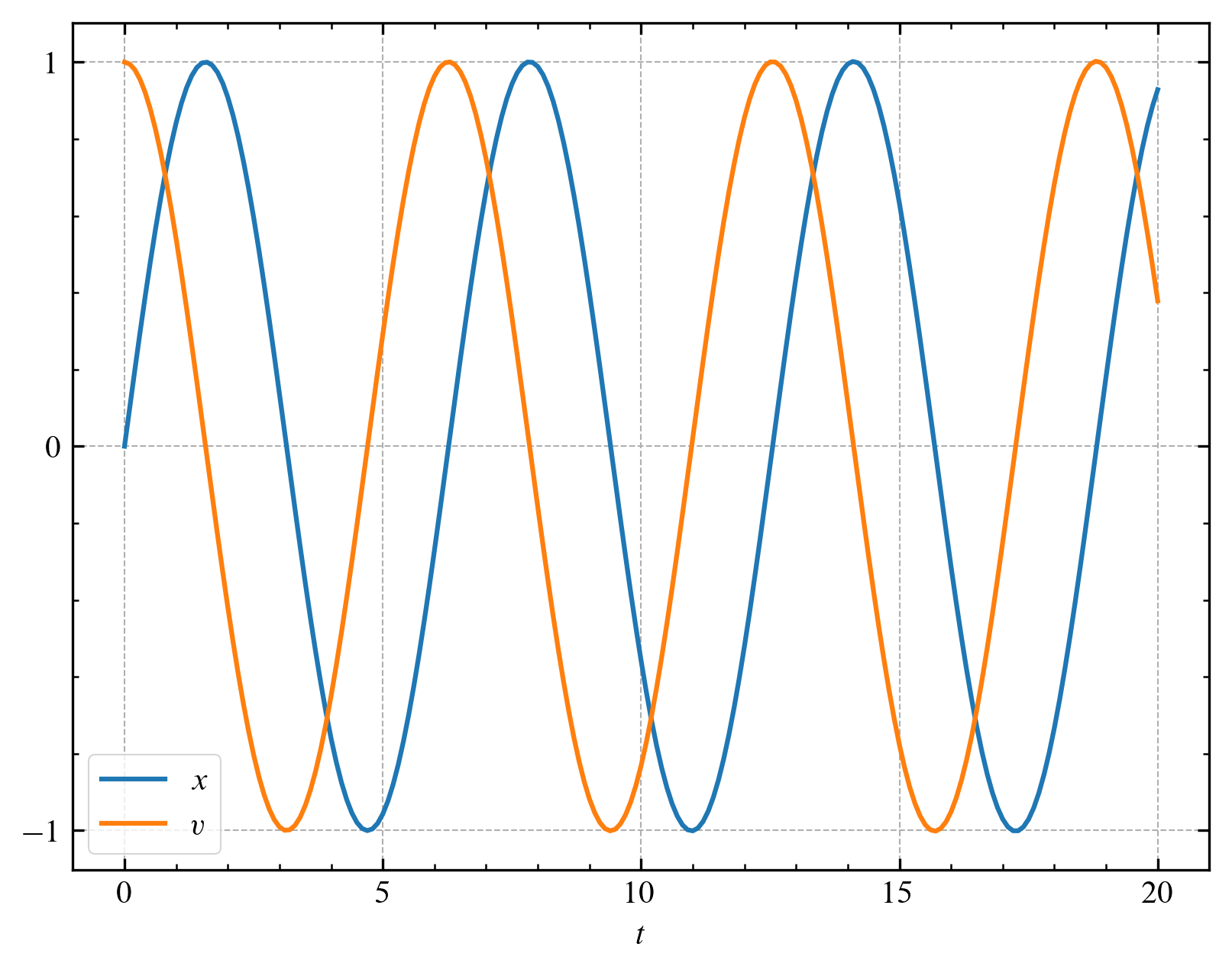 마찬가지로 정확한 해와의 상대 오차를 계산하면 시간 간격이 $1/10$배가 될 때 오차는 $10^{-2}$배가 됨을 알 수 있습니다.
마찬가지로 정확한 해와의 상대 오차를 계산하면 시간 간격이 $1/10$배가 될 때 오차는 $10^{-2}$배가 됨을 알 수 있습니다.
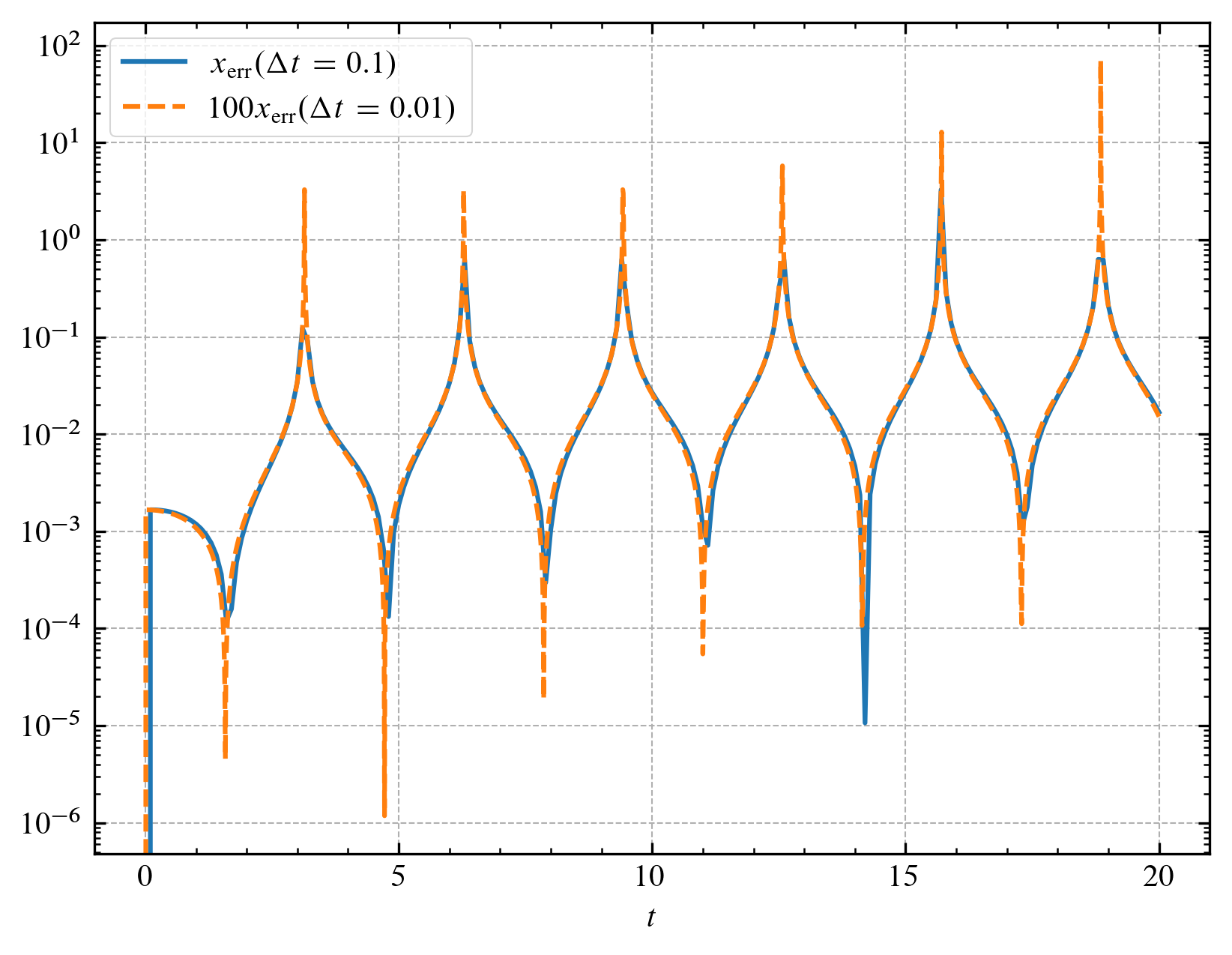 $2$차 정확도를 가지는 방법은 앞서 소개한 $2$차 Runge-Kutta 방법 외에 modified Euler 방법 등 여러가지가 있습니다.
$2$차 정확도를 가지는 방법은 앞서 소개한 $2$차 Runge-Kutta 방법 외에 modified Euler 방법 등 여러가지가 있습니다.
4th-order Method
위와 비슷한 방법으로 Runge-Kutta 방법을 $4$차 정확도까지 확장할 수 있습니다. 다음은 잘 알려진 $4$차 Runge-Kutta 방법입니다.
$$
\begin{align*}
\bold{k}_1 &= f(t_n, \bold{y}_n) \Delta t \\
\bold{k}_2 &= f(t_{n + 1/2}, \bold{y}_n + \bold{k}_1 / 2) \Delta t\\
\bold{k}_3 &= f(t_{n + 1/2}, \bold{y}_n + \bold{k}_2 / 2) \Delta t\\
\bold{k}_4 &= f(t_{n + 1}, \bold{y}_n + \bold{k}_3) \Delta t\\
\bold{y}_{n+1}&= \bold{y}_n + (\bold{k}_1 + 2 \bold{k}_2 + 2 \bold{k}_3 + \bold{k}_4) / 6 + \mathcal{O}(\Delta t^5)
\end{align*}
$$
여기서 $f(t, \bold{y})$는 $t$, $\bold{y}$에서 계산한 $\bold{y}'$입니다.
이를 파이썬 코드로 구현하면 다음과 같습니다.
def rk4(dt=0.1, it=200):
# Set time step interval, initial t, y = [x, v]
# dt = 0.1
t = 0
y = np.array([0.0, 1.0])
# SHO. x_dot = v, y_dot = -x
def y_dot(t, y):
return np.array([y[1], -y[0]])
# To store data
T = [t]
X = [y[0]]
V = [y[1]]
# Iteration using RK4 Method
for n in range(it):
t += dt
k1 = y_dot(t, y) * dt
k2 = y_dot(t + dt / 2, y + k1 / 2) * dt
k3 = y_dot(t + dt / 2, y + k2 / 2) * dt
k4 = y_dot(t + dt, y + k3) * dt
y += (k1 + 2 * k2 + 2 * k3 + k4) / 6
T.append(t)
X.append(y[0])
V.append(y[1])
return np.array(T), np.array(X), np.array(V)
이전과 같은 조건으로 시간 간격 $0.1$로 적분하였을 때의 모습입니다.
육안상으로는 $2$차 방법과 거의 동일해보입니다.
 상대 오차를 계산한 결과 정확도가 $10^4$배 차이남을 확인할 수 있습니다.
상대 오차를 계산한 결과 정확도가 $10^4$배 차이남을 확인할 수 있습니다.
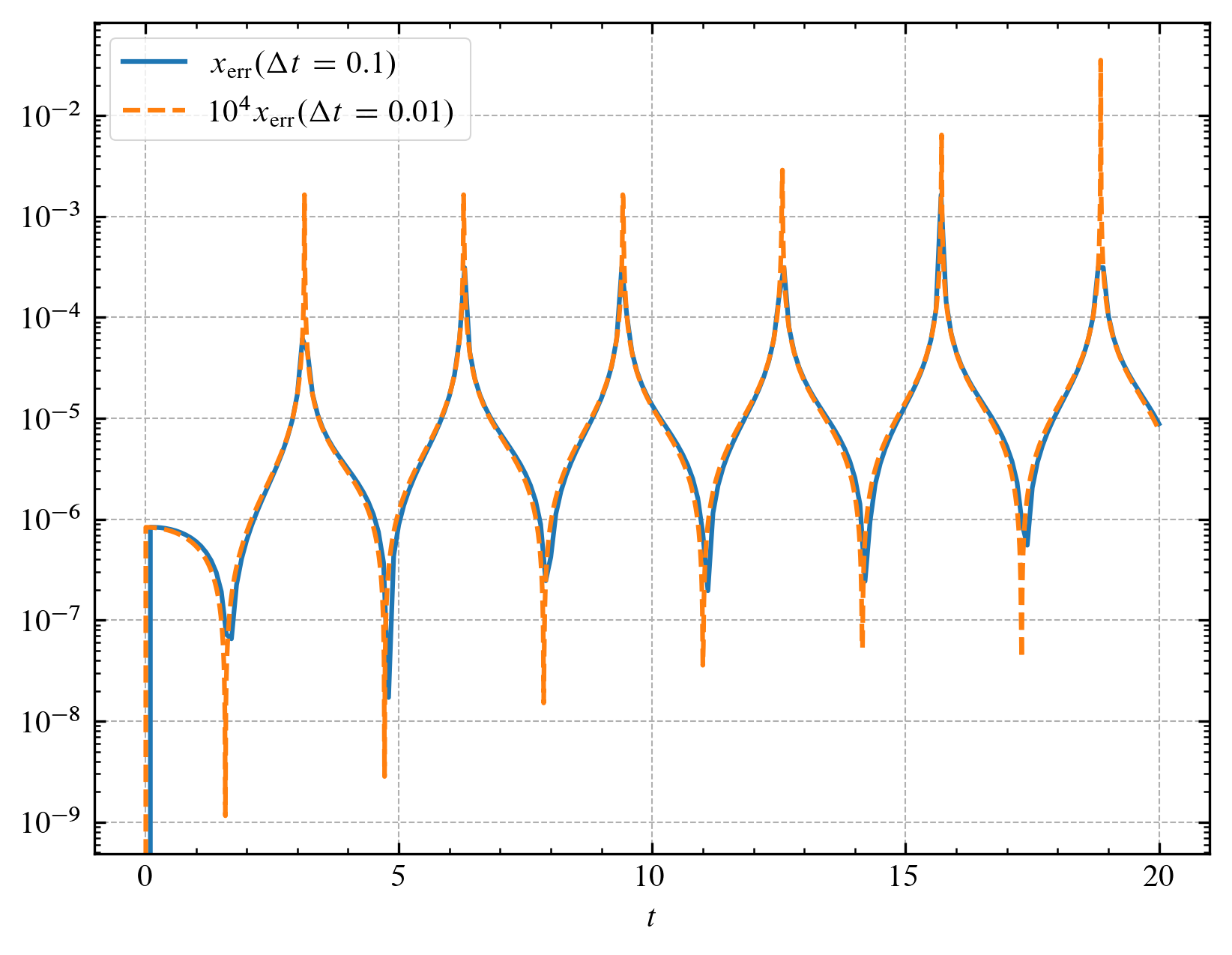
y_dot 함수를 수정하면 다른 미분 방정식의 해를 구할 수도 있습니다.
예를 들어 속도에 의존하는 감쇠력 $f=-bv$를 받는 진자 운동을 고려해봅시다.
감쇠 계수damping parameter $\beta = b / 2m$, 고유 각진동수 $\omega_0 = \sqrt{k/m}$을 사용하여 미분 방정식을 나타내면 다음과 같습니다:
$$
\frac{d^2x}{dt^2} + 2\beta \frac{dx}{dt} + \omega_0^2 x = 0.
$$
$v = dx/dt$를 이용하여 두 개의 방정식으로 분리하면,
$$
\frac{dx}{dt} = v, \quad \frac{dv}{dt} = - 2\beta v - \omega_0^2 x.
$$
$k=m=1$로 스케일링하면 $\omega_0$ 또한 $1$입니다.
이제 코드는 다음과 같이 수정됩니다.
def rk4_ocs(x_0=1.0, v_0=0.0, beta=1.0, dt=0.1, it=200):
# Set time step interval, initial t, y = [x, v]
t = 0
y = np.array([x_0, v_0])
# Damping Oscillation
def y_dot(t, y):
return np.array([y[1], -2 * beta * y[1] - y[0]])
# To store data
T = [t]
X = [y[0]]
V = [y[1]]
# Iteration using Euler Method
for n in range(it):
t += dt
k1 = y_dot(t, y) * dt
k2 = y_dot(t + dt / 2, y + k1 / 2) * dt
k3 = y_dot(t + dt / 2, y + k2 / 2) * dt
k4 = y_dot(t + dt, y + k3) * dt
y += (k1 + 2 * k2 + 2 * k3 + k4) / 6
T.append(t)
X.append(y[0])
V.append(y[1])
return np.array(T), np.array(X), np.array(V)
$\beta^2 = \omega_0^2$일 때 진자는 임계 감쇠critical damping합니다.
다음 그림은 $\beta = 1 (=\omega_0)$일 때의 결과를 나타낸 것입니다.
 $\beta^2 > \omega_0^2$일 때 진자는 과대 감쇠overdamping합니다.
다음 그림은 $\beta = 2$일 때의 결과를 나타낸 것입니다.
$\beta^2 > \omega_0^2$일 때 진자는 과대 감쇠overdamping합니다.
다음 그림은 $\beta = 2$일 때의 결과를 나타낸 것입니다.
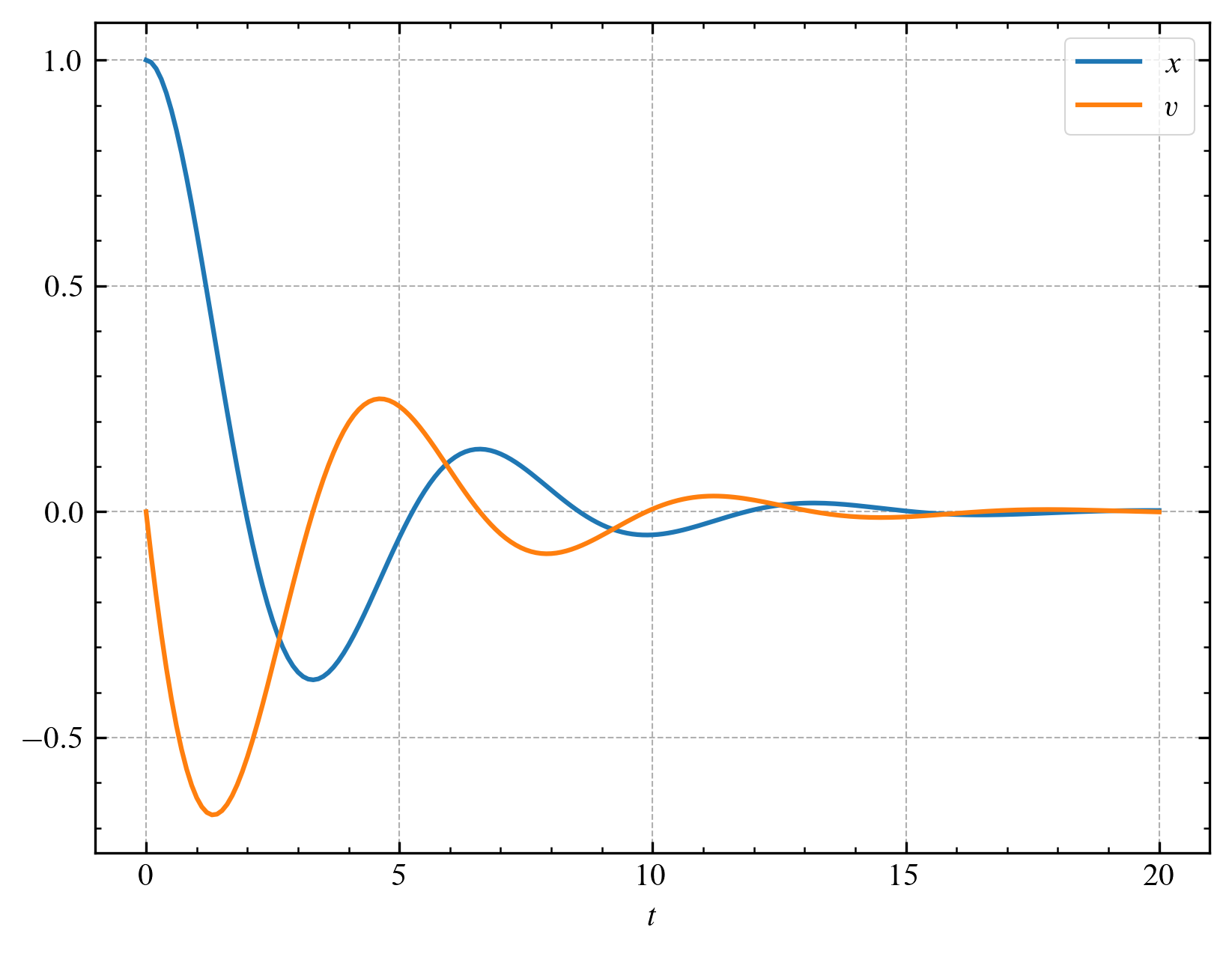
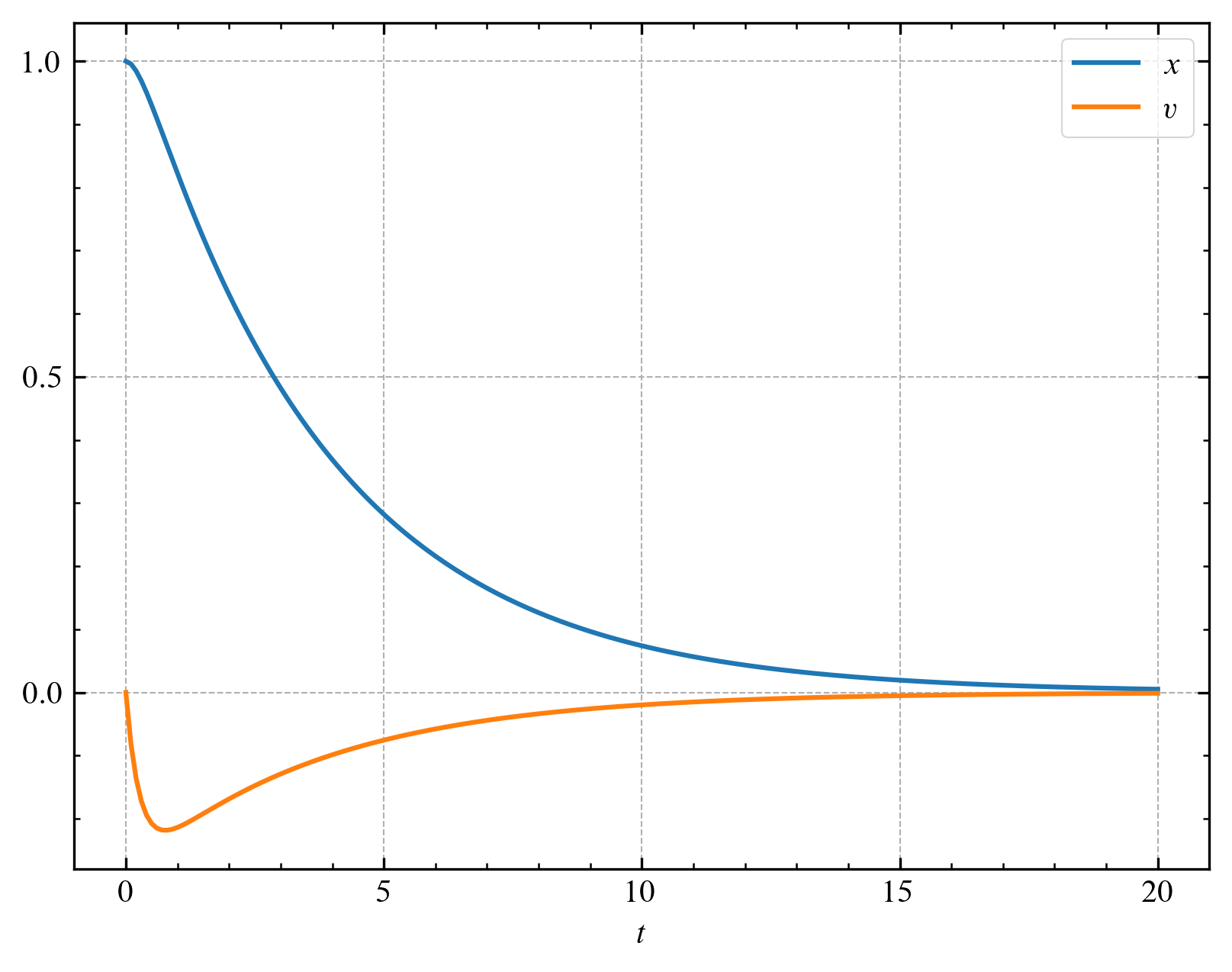 $\beta^2 < \omega_0^2$일 때 진자는 과소 감쇠underdamping합니다.
다음 그림은 $\beta = 0.3$일 때의 결과를 나타낸 것입니다.
$\beta^2 < \omega_0^2$일 때 진자는 과소 감쇠underdamping합니다.
다음 그림은 $\beta = 0.3$일 때의 결과를 나타낸 것입니다.
 위의 결과를 이미 알려진 정확한 해와 비교함으로써 정확성을 확인할 수 있습니다.
하지만 어떤 방정식의 경우 정확한 해가 알려져있지 않을 수도 있습니다.
이때 결과가 정확한 지 확인할 수 없어도 그 수렴성을 확인할 수 있는 방법이 있습니다.
위의 결과를 이미 알려진 정확한 해와 비교함으로써 정확성을 확인할 수 있습니다.
하지만 어떤 방정식의 경우 정확한 해가 알려져있지 않을 수도 있습니다.
이때 결과가 정확한 지 확인할 수 없어도 그 수렴성을 확인할 수 있는 방법이 있습니다.
Convergence Test
$\bold{y}_n$에서 테일러 전개하여 $\Delta t$를 대입하면 다음 $\bold{y}_{n+1}$을 얻을 수 있습니다.
$$
\bold{y}_{n+1}^\text{ext} = \bold{y}_n + \bold{y}_n'\Delta t + \frac{1}{2}\bold{y}_n''\Delta t^2 + \frac{1}{6}\bold{y}_n'''\Delta t^3 + \frac{1}{24}\bold{y}_n''''\Delta t^4 + \frac{1}{120}\bold{y}_n'''''\Delta t^5 + \cdots.
$$
테일러 전개의 모든 항을 사용할 때 $\bold{y}_{n+1}^\text{ext}$를 얻을 수 있지만, 수치 계산에서 모든 항을 구하기는 불가능합니다.
대신 앞에서 다뤘던 $N$차 정확도를 가지는 여러 방법들을 사용하면 테일러 전개의 $\Delta t^{N}$항 까지는 정확하게 반영합니다.
$$
\bold{y}_{n+1}^{N\text{th-order}} = \bold{y}_n + \bold{y}_n'\Delta t + \frac{1}{2}\bold{y}_n''\Delta t^2 + \cdots + \frac{1}{N!}\bold{y}_n^{(N)}\Delta t^N + \mathcal{O}(\Delta t^{N+1}).
$$
따라서 수치적으로 구한 해와 정확한 해의 차는
$$
\bold{y}_{n+1}^\text{ext} - \bold{y}_{n+1}^{N\text{th-order}} = a\Delta t^{N+1} + \mathcal{O}(\Delta t^{N+2}).
$$
여기서 $a$는 적절한 상수입니다.
이제 $\Delta t \to \frac{\Delta t }{K}$로 시간 간격을 $K$등분한다면 한 스텝 후 오차는
$
a\left(\frac{\Delta t}{K}\right)^{N + 1}
$
이 되며 $K$ 스텝 후 오차는
$
\frac{a}{K^{N}}\Delta t ^{N+1}
$
이 되어 누적 오차가 $1/K^N$배가 됩니다.
$$
\bold{y}_{n+1}^\text{ext} - \bold{y}_{n+1}^{N, K} = \frac{a}{K^N}\Delta t^{N+1} + \mathcal{O}(\Delta t^{N+2}).
$$
실제로 $\bold{y}_{n+1}^\text{ext}$을 모르는 상황에서 $K = K_1, K_2$에 대한 위의 두 식을 빼주면
$$
\bold{y}_{n+1}^{N, K_2} - \bold{y}_{n+1}^{N, K_1} = a\left(\frac{1}{K_1^N} - \frac{1}{K_2^N}\right)\Delta t^{N+1} + \mathcal{O}(\Delta t^{N+2}).
$$
또한 우리는 $a$를 모르기 때문에 $K=K_2, K_3$에 대한 식이 필요합니다.
$$
\bold{y}_{n+1}^{N, K_3} - \bold{y}_{n+1}^{N, K_2} = a\left(\frac{1}{K_2^N} - \frac{1}{K_3^N}\right)\Delta t^{N+1} + \mathcal{O}(\Delta t^{N+2}).
$$
이제 두 식을 나누면 $a$를 소거할 수 있습니다.
$$
\frac{\bold{y}_{n+1}^{N, K_2} - \bold{y}_{n+1}^{N, K_1}}{\bold{y}_{n+1}^{N, K_3} - \bold{y}_{n+1}^{N, K_2}}
\approx \frac{\frac{1}{K_1^N} - \frac{1}{K_2^N}}{\frac{1}{K_2^N} - \frac{1}{K_3^N}}.
$$
$K_1, K_2,K_3$ 대신 시간 간격 $\Delta t_1$, $\Delta t_2$, $\Delta t_3$로 식을 다시 쓰면
$$
\frac{\bold{y}_{n+1}^{N, \Delta t_2} - \bold{y}_{n+1}^{N, \Delta t_1}}{\bold{y}_{n+1}^{N, \Delta t_3} - \bold{y}_{n+1}^{N, \Delta t_2}}
\approx \frac{\Delta t_2^N - \Delta t_1^N}{\Delta t_3^N - \Delta t_2^N}.
$$
앞서 해보았던 $\beta = 0.3$ 과소 감쇠 진자 운동에 적용해보겠습니다.
시간 간격이 각각 $0.1$, $0.2$, $0.3$일 때 위의 식에 대입해보면
$$
\frac{0.2^4 - 0.1^4}{0.3^4 - 0.2^4} \approx 0.231.
$$
따라서 이 수를 $|x_3 - x_2|$에 곱하였을 때의 값이 $|x_2 - x_1|$의 값과 다음 그림과 같이 일관성이 있어야 합니다.
시간 간격이 다른 두 데이터의 차를 바로 구할 수 없기 때문에 $3$차 스플라인 보간을 사용하였습니다.

Copyright 2023ⓒ D.C. Kim. All Rights Reserved.
 처음에는 진폭이 거의 $1$에 가까운 운동을 보였지만 시간이 지날수록 진폭이 점점 증가하는 모습을 볼 수 있습니다.
시간 간격 $\Delta t$를 줄이면 더 정확한 결과를 얻을 수 있습니다.
다음 그림은 위와 같은 조건에서 $\Delta t$를 $1/10$배로 하고 반복 횟수는 $10$배로 한 모습을 나타낸 것입니다.
처음에는 진폭이 거의 $1$에 가까운 운동을 보였지만 시간이 지날수록 진폭이 점점 증가하는 모습을 볼 수 있습니다.
시간 간격 $\Delta t$를 줄이면 더 정확한 결과를 얻을 수 있습니다.
다음 그림은 위와 같은 조건에서 $\Delta t$를 $1/10$배로 하고 반복 횟수는 $10$배로 한 모습을 나타낸 것입니다.
 우리는 위 방정식의 해가 $x_\mathrm{ext} = \sin t$, $v_\mathrm{ext} = \cos t$임을 알고 있으므로
상대 오차 $x_\mathrm{err} = |\frac{x - x_\mathrm{ext}}{x_\mathrm{ext}}|$,
$v_\mathrm{err} = |\frac{v - v_\mathrm{ext}}{v_\mathrm{ext}}|$ 또한 나타낼 수 있습니다.
다음 그림은 각각 $\Delta t$가 $0.1$, $0.01$일 때 $x$, $v$의 상대 오차를 나타낸 것입니다.
우리는 위 방정식의 해가 $x_\mathrm{ext} = \sin t$, $v_\mathrm{ext} = \cos t$임을 알고 있으므로
상대 오차 $x_\mathrm{err} = |\frac{x - x_\mathrm{ext}}{x_\mathrm{ext}}|$,
$v_\mathrm{err} = |\frac{v - v_\mathrm{ext}}{v_\mathrm{ext}}|$ 또한 나타낼 수 있습니다.
다음 그림은 각각 $\Delta t$가 $0.1$, $0.01$일 때 $x$, $v$의 상대 오차를 나타낸 것입니다.

 사용한 Euler 방법이 $1$차 정확도를 가지므로 둘의 차이는 대략 $10^{1}$배입니다.
사용한 Euler 방법이 $1$차 정확도를 가지므로 둘의 차이는 대략 $10^{1}$배입니다.

 마찬가지로 정확한 해와의 상대 오차를 계산하면 시간 간격이 $1/10$배가 될 때 오차는 $10^{-2}$배가 됨을 알 수 있습니다.
마찬가지로 정확한 해와의 상대 오차를 계산하면 시간 간격이 $1/10$배가 될 때 오차는 $10^{-2}$배가 됨을 알 수 있습니다.
 $2$차 정확도를 가지는 방법은 앞서 소개한 $2$차 Runge-Kutta 방법 외에 modified Euler 방법 등 여러가지가 있습니다.
$2$차 정확도를 가지는 방법은 앞서 소개한 $2$차 Runge-Kutta 방법 외에 modified Euler 방법 등 여러가지가 있습니다.
 상대 오차를 계산한 결과 정확도가 $10^4$배 차이남을 확인할 수 있습니다.
상대 오차를 계산한 결과 정확도가 $10^4$배 차이남을 확인할 수 있습니다.

 $\beta^2 > \omega_0^2$일 때 진자는 과대 감쇠overdamping합니다.
다음 그림은 $\beta = 2$일 때의 결과를 나타낸 것입니다.
$\beta^2 > \omega_0^2$일 때 진자는 과대 감쇠overdamping합니다.
다음 그림은 $\beta = 2$일 때의 결과를 나타낸 것입니다.
 $\beta^2 < \omega_0^2$일 때 진자는 과소 감쇠underdamping합니다.
다음 그림은 $\beta = 0.3$일 때의 결과를 나타낸 것입니다.
$\beta^2 < \omega_0^2$일 때 진자는 과소 감쇠underdamping합니다.
다음 그림은 $\beta = 0.3$일 때의 결과를 나타낸 것입니다.
 위의 결과를 이미 알려진 정확한 해와 비교함으로써 정확성을 확인할 수 있습니다.
하지만 어떤 방정식의 경우 정확한 해가 알려져있지 않을 수도 있습니다.
이때 결과가 정확한 지 확인할 수 없어도 그 수렴성을 확인할 수 있는 방법이 있습니다.
위의 결과를 이미 알려진 정확한 해와 비교함으로써 정확성을 확인할 수 있습니다.
하지만 어떤 방정식의 경우 정확한 해가 알려져있지 않을 수도 있습니다.
이때 결과가 정확한 지 확인할 수 없어도 그 수렴성을 확인할 수 있는 방법이 있습니다.
